Understanding the Basic Elements

Arguments consist of three basic elements: premises, inferences, and conclusions.

Using Premises

Premises are statements assumed to be true and presented as evidence in support of a claim. The argument does not try to prove the truth of a premise but just takes it to be true:

The two premises above are assumed to be true. The argument does not try to prove the premises but rather uses them to draw its conclusion or claim.

Drawing Inferences and Conclusions

An inference is a statement that is derived from previous statements—whether premises or other inferences. The truth of an inference is based on both the truth of the previous statements and on the way the inference is derived.

The inference that Anya has passed calculus is based on premises 1 and 2. If Anya has an engineering degree and all engineers have to pass calculus, Anya must have passed calculus.

A conclusion is simply the final inference, derived from previous statements. Here, the concluding inference is that if Anya has passed calculus, she must understand it. A conclusion can become a premise in a new argument.

Understanding Logical Rules

Classical logic has created a set of rules for indicating a statement's truth.

Three Classic Laws of Thought

The Greek philosopher Aristotle determined the following three rules of logic:

Four Basic Propositions

To put ideas into categories, Aristotle came up with four basic propositions. (Proposition refers to the content or meaning of a sentence.) Propositions that are diagonal contradict each other, as do the top two propositions.

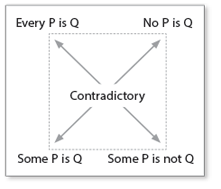
1. Universal affirmative: Every P is Q.
   • Every kangaroo is a marsupial.
2. Universal negative: No P is Q.
   • No kangaroo is a marsupial.
3. Particular affirmative: Some P is Q.
   • Some kangaroos are marsupials.
4. Particular negative: Some P is not Q.
   • Some kangaroos are not marsupials.

 

Three Function Words

Two thousand years after Aristotle, George Boole came up with a system for testing the truth of a claim using three basic words.

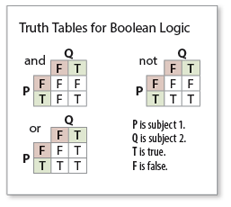
1. And: P and Q (Both must be true for the statement to be true.)
   • Sarah and Janelle are astronomers.
2. Or: P or Q (One must be true for the statement to be true.)
   • Sarah or Janelle is an astronomer.
3. Not: P not Q (P must be true for the statement to be true.)
   • Sarah, not Janelle, is an astronomer.

 

Nine Inference Rules

In addition to rules about the truth or falsity of a statement, classical logic includes a set of rules for making inferences and conclusions. As you develop your logical arguments, use the rules below to make inferences.