up
101

Creating Mathematical Proofs

A geometric proof works very much like the arguments you have been studying so far. A proof begins with a set of givens—things that are known, including information provided within a graphic. The proof then asks you to prove a specific conclusion. Use a two-column approach. In the first column, write a series of statements—premises (givens), inferences, and conclusions. In the second column, indicate the reason for each statement. Here’s an example.

Given: AB || DC and AD || BC (lines AB and DC are parallel; lines AD and BC are parallel)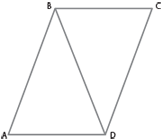Parallelogram

Prove: ∠BAD = ∠BCD (angles BAD and BCD are equal)

Statements

Reasons

  1. AB || DC

Given

  1. ∠ABD = ∠BDC

Alternate interior angles are equal.

  1. AD || BC

Given

  1. ∠ADB = ∠DBC

Alternate interior angles are equal.

  1. ∠ADB + ∠ABD + ∠BAD = 180

Angles of triangle = 180.

  1. ∠BDC + ∠DBC + ∠BCD = 180

Angles of triangle = 180.

  1. ∠ADB + ∠ABD + ∠BAD = ∠BDC + ∠DBC + ∠BCD

Substitution of equivalent amounts.

  1. ∠BAD = ∠BCD

Substitution of equivalent amounts.

 

Discussion: The student recognized that line BD was crossing parallel lines AB and DC as well as parallel lines AD and BC. The student also knew that a line that crosses parallel lines makes the same acute angle with one line as with the other. That one rule applied twice showed that triangle ABD had two of the same angles as triangle BCD. Since all angles of a triangle add up to 180, the student could prove that the final angles were equal—that ∠BAD = ∠BCD.

Your Turn Which of the statements in the argument above are premises? Which are inferences? Which is a conclusion? Is this proof deductive or inductive? Does it guarantee its conclusion?

Math and Language Arts: Respond to each prompt:

  1. Write a mathematical symbol that means “and.”
  2. Write a mathematical symbol that means “is.”
  3. Write the following as a mathematical statement: Jason and Jana are a couple.
  4. How are sentences with linking verbs like equations?
 
up